数学は楽しい!どのように数学を学ぶか
数年前にビジネスマンの間で数学ブームが起こりましたね.「数学=論理的」であるため,「数学ができる→論理的思考ができる→仕事ができるようになる」というロジックがよく謳われていましたが,このロジックには疑問を感じていました.というのも,数学で求められる論理性とビジネスで求められる論理性は次元が違いますし,ビジネスは論理だけでは動かないからです(仕事のために数学を学ぶのが悪いと言っているのではなく,数学を勉強すれば仕事ができるようになる,というのは違うのではないか,と言いたいだけです).
ただ最近は,純粋に数学を楽しもうとする大人も増えているようで,それはとても良いことだと思います.理学部の人のように数学を専攻したわけではないので,そこまで深い知識があるわけではないですが,私も大学で数学を学び,今でも数学の本を読むことがあります.ちょっと,私が考える数学の勉強の仕方について書いてみますので,これから数学を勉強してみよう,という人の参考になれば嬉しいです.
これから書く内容は大学で学ぶ数学の分野が中心ですが,数学への向き合い方について書いているため,中学・高校の数学からやり直そうとしている人も参考にしてもらえると嬉しいです.
数学には色々な基礎分野がありますが,大きく2つに分けることができると思っています.それは 演習が大切な分野 と 思考が大切な分野 の2つです.
演習が大切な分野
これに分類される具体的な分野としては次のような分野です.
- 微積
- 線形代数
- 微分方程式・偏微分方程式
- 複素関数論
- フーリエ解析
- 統計学・確率
この分野で大切なことは式が与えられた時に自分で計算を進めることができることです.例えば,今流行りの統計の分野など,例えば中心極限定理などの意味を知っているよりも,実際のデータを前にした時に手を動かして考察を下せる状態にある方がよほど大事です.これらの分野はツール的な側面が強いので,ツールを上手く使えるように,何度も練習することが大切です.
また,これら演習系分野では公式が沢山出てきますが,公式は暗記するのではなく,自分で導出することが大切です.導出された道筋を遡り,自分で理解したうえで,必要な物は覚える,この流れです.
受験数学は暗記,という人がいますが,確かにそれは否定出来ません.しかし,公式がどのように導かれ,どのように一般化されたのかを理解しなければ本当の記憶にはならないと思います.大人が学ぶ数学は,試験で点数をつけられることはないので,腹落ちするまでしっかりと向き合うといいと思います.
思考が大切な分野
具体的な分野はとしては,
- 集合・位相
- 測度論
- 確率論
あたりです.
この分野では,数式が出てくるよりも抽象的な議論が続くことが多いため,用語の定義を自分の腹に落とし込んで理解し,その上で議論や証明の筋を沿ってみることが大切と思います(正直,私はこれらの分野は弱いので,あまり詳しく書けません…).
例えば,ロシアの数学者ペレルマンが解いて有名になったポアンカレ予想は位相幾何学(トポロジー)の問題ですが,その内容は難解で,言葉の定義が理解できていないと問題の意味もよくわかりません.
私もトポロジーは殆ど忘れてしまったため,大学の時に読んだテキストをまた一から読み直しています….
そして数学は積み上げの学問ですので,学ぶ順番も大切です.ある分野を学ばないと次に進めない,ということは往々にしてあります.私が思う学ぶ順番は
微積 線形 → 集合・位相
をまず始めにやり,あとは,演習系,思考系分野を上から順番に進めていくのがいいかと思います.最近流行りの統計学は独立しているので,好きな時に学べます.ただ,それでも微積と線形を先に学ぶ必要があります.何はともあれ,まずは微積と線形です.
数学を楽しむには,確かに最初のハードルは高いです.でも,それを超えると一気に視界が開けます.ゆっくりでも,少しずつ数学の世界を旅してみましょう!!
[adchord]


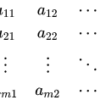


ディスカッション
コメント一覧
まだ、コメントがありません