Pythonでポートフォリオのリスクを計算してみた
自分のポートフォリオのリスクとリターンってどれくらいかって気になりませんか?
私はめっちゃ気になっていながらも計算を先延ばしにしていたのですが,コロナショックの相場変動もあり,ここらで一度把握せなあかんなと思い,一念発起して計算することにしました.
計算にはPythonとExcelを使いました.
ステップは多いですが,順を追って書いていますので,自分で計算してみたいという人の参考になれば幸いです.
計算前提
まずは今回の計算における前提ですが,
計算期間:2006年から2020年3月31日までの14年3ヶ月で計算
です.
リーマン・ショックとコロナショックは含まないとリスクを過小評価してしまうので,この期間にしました.
ステップ1 銘柄の株価を取得する
PythonのPandasを使い,Yahoo Financeから株価データを取得し,それをcsvファイルに格納します.
サーバーに負担をかけないよう,銘柄ごとに1秒間の待機時間を設けています.
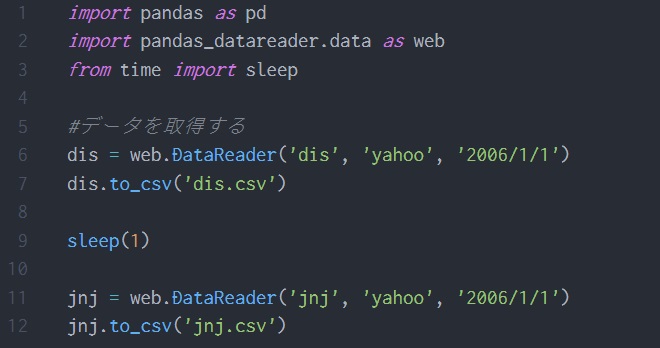
Yahoo FinanceからPythonで株価データが取れなくなったというのを聞いたことがありますが,問題なく取れました.
ステップ2 銘柄リターンと期待リターンを計算する

株価が取れたら,各年のリターンを計算して銘柄毎に算術平均を出します,これが銘柄ごとの期待リターンです.
ポートフォリオの期待リターンは銘柄の割合と期待リターンの線形結合のため,エクセルのSUMPRODUCT関数を使えば簡単に計算できます.
私のポートフォリオの期待リターンは11.5%です.
期待リターンは簡単で,これで終わりです.
ステップ3 共分散行列の作成
続いて鬼門のリスクの計算です.
誰だか忘れましたが,「証券,ポートフォリオの期待リターンの計算はあまり意味がないが,リスクの計算は大いに意味がある」と言っている有名な投資家がいました.
計算は複雑な分,得るものが多いのでしょうか.
ポートフォリオのリスクを計算するには,銘柄ごとの分散と共分散が必要で,そのために共分散行列を作る必要があります.
共分散行列は数式で表すと次のようになります.
$$begin{eqnarray}
Sigma = left(
begin{array}{cccc}
Cov_{11} & Cov_{12} & ldots & Cov_{1n} \
Cov_{21} & Cov_{22} & ldots & Cov_{2n} \
vdots & vdots & ddots & vdots \
Cov_{n1} & Cov_{n2} & ldots & Cov_{nn}
end{array}
right)
end{eqnarray}$$
同じものの共分散は分散に等しいので,主対角線は分散になるため,分散共分散行列とも言われますが,同じものです.
この記事では共分散行列で統一します.
ステップ2で添付している,銘柄ごとのリターンを示した行列があればエクセルでも共分散行列を作ることはできますが,かなり面倒です.
なので,ここでもPythonでやっちゃいましょう,Pythonなら一行のコードで共分散行列が作れます.
コードはこちら,ドン.
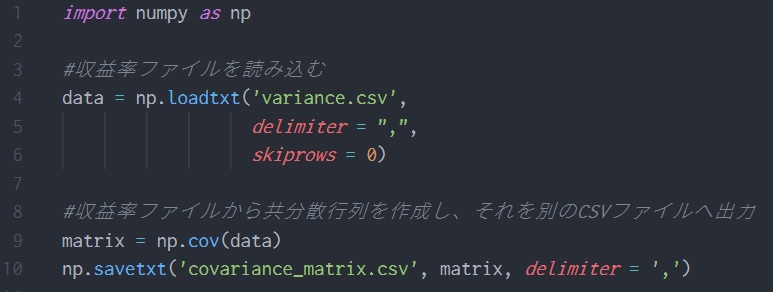
まず,年度ごとの収益率を書き込んだCSVファイル(ここではvariance.csv)を読み込みます.
肝はnp.covで,Pythonはこの一行で共分散行列を作成してくれます.
私はこのコードを知った時,震えるほど感動しました.
なお,Pythonは相関行列もCorrcoefの一行で作ってくれます,もう,Pythonのない世界は考えられません.
できあがった共分散行列がこちらです(共分散行列は対称行列のため,私は重複部分を消しましたが,np.covでは全ての数字が入ってきます).
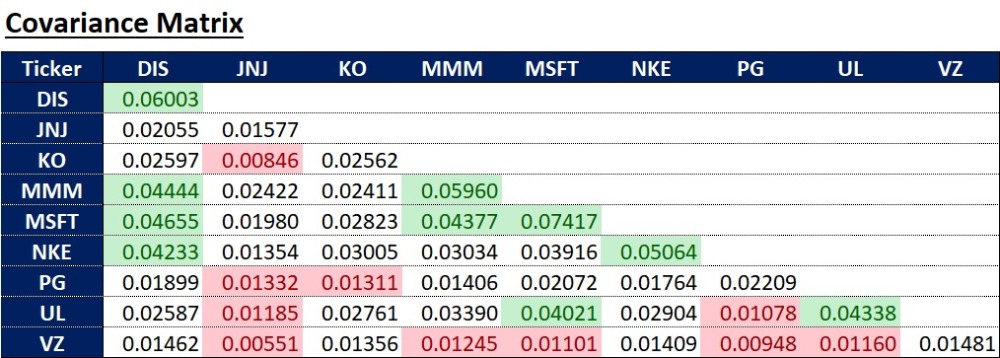
ここでちょっと横道にそれますが,共分散行列から得られる気付きについて書いてみたいと思います.
ポートフォリオのリスク計算とは直接関係ないので,急ぐ人はステップ4まで飛ばしてください.
こうやって共分散行列を眺めると,これって貴重なデータだなぁとつくづく思います.
数字が大きいものを緑,小さいものを赤で識別していますが,これを見るとJNJ, KO, PG, VZの分散が小さいことがわかります.
これらはディフェンシブ銘柄の代表格で,ディフェンシブ銘柄はリターンの変動が小さいと言われていますが,実際のデータからもそれを確認できます.
一方,DIS, MMM, NKEは景気サイクルと連動するため変動が大きくなるイメージですが,それがしっかりと分散に表れています.
また,VZの行に多くの赤がありますが,これはVZのリターンが他の銘柄とあまり相関を持たないことを意味します.
通信はもはやインフラなので,景気変動に依存せず,独立して動いているということでしょうか,分散も個別銘柄のなかで一番小さいですし.
ポートフォリオの分散化から,共分散がマイナスの銘柄を組み込みたいのですが,ここ数年は米国株が総じて強気だったので,そのような銘柄を探すのは難しそうです.
ステップ4 ポートフォリオのリスク計算
ポートフォリオのリスクを計算するには,ポートフォリオ収益率の分散を計算して,それの平方根を取ればOKです.
言葉でいうと簡単ですが,
数式は
$$sigma_{p}^2 = w_{1}^2sigma_{1}^2 + w_{2}^2sigma_{2}^2 + ldots + w_{n}^2sigma_{n}^2 + 2(w_{1}w_{2}sigma_{12} + w_{1}w_{3}sigma_{13} + ldots + w_{n-1}w_{n}sigma_{n-1n})$$
となり,かなり煩雑な計算が必要です(wはその証券が占める構成割合です).
前半部分の計算は比較的簡単で,下のような表を作ればエクセルでも簡単に計算できて,この例では0.0051です.
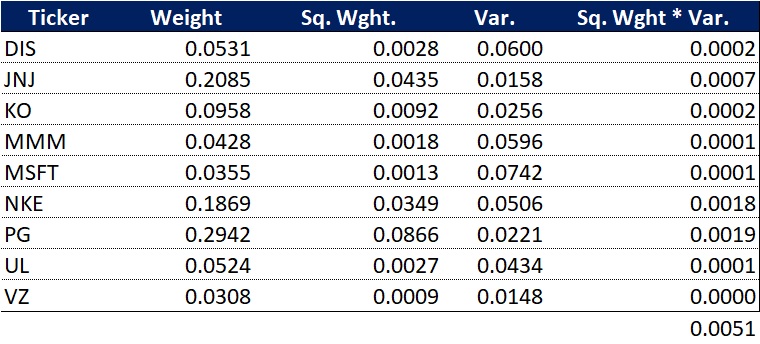
残りの項は,Pythonで作った共分散行列を活用して計算し,この例では0.01486です,2倍するのを忘れないようにします.
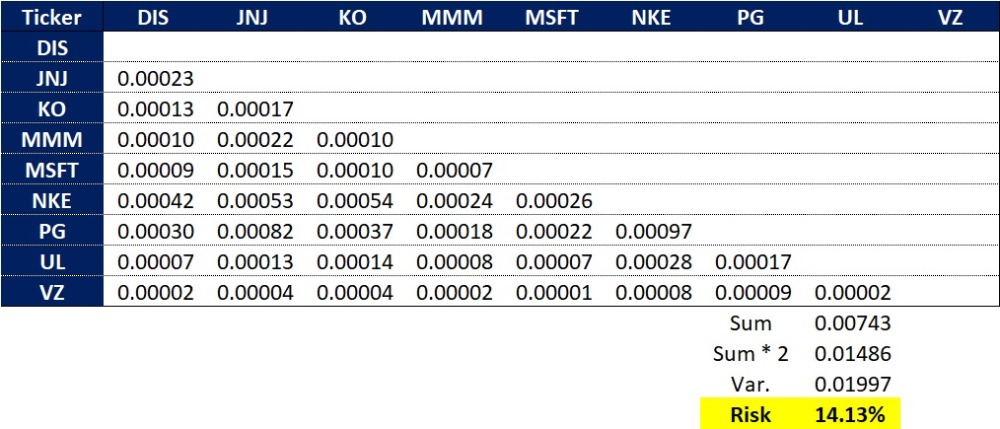
合計の0.01997ですが,リスクは標準偏差なので平方根を取って14.13%となります.
長い道のりでしたが,とうとうポートフォリオのリスクにたどり着きました.
まとめ ポートフォリオ評価
私のポートフォリオは期待リターン11.5%,リスク14.13%でした.
リターンについては,リーマン・ショックとコロナショック(こちらはまだ終息してませんが)を経験しながらも,平均するとこれだけのリターンを毎年出してくれてきたというのは頼もしいです.
ただ,気をつけなければいけないのは,これは今後のリターンを全く保証しません.
その意味でも,期待リターンはあくまで参考値です.
リスク14.13%はどう評価すべきでしょうか.
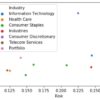
個別証券のリスクを見ると,一番小さいのがVZで12.2%ですが,20%を超えている銘柄も多いです.
特にDIS, MMM, MSFT, NKEが高くて,それぞれ24.5%, 24.4%, 27.2%, 22.5%です.
これらをブレンドすることでリスクを14.13%まで低減させることができているので,分散化の効果は出ていると評価できると思います.
以上,ポートフォリオのリターンとリスク計算,いかがでしたでしょうか.
今回はちょっとマニアックな内容でしたが,私はこんなことを考えるのが大好きです.
次はどんな構成割合にすればいちばんリスクを減らせるかという最適化問題をボチボチ取り組んで行きたいと思います.
さて,頭を使って疲れたから走りにでも行こうかな.
それでは,また.





ディスカッション
コメント一覧
まだ、コメントがありません